Network Optimization

Network optimization is a critical area in computational design, focusing on creating efficient and cost-effective connections among a set of points. It can be used to solve problems in escape routes, transportation, urban planning, and more. Among the key concepts in network optimization are Minimal Path Networks, the Steiner Tree Problem, and Relative Neighborhood Graphs.

Relative Neighborhood Graph (RNG)

Relative Neighborhood Graphs (RNGs) connect points based on their relative proximity, ensuring that an edge is drawn between two points if no other point is closer to both. This concept helps create sparse networks that emphasize local connections, which can then be used as a foundation for further optimization.

Animation of a Relative Neighborhood with four anchor points at the corners

Minimal Path Networks

Also known as shortest path networks, they are fundamental in ensuring that a network connecting multiple points is as short as possible. For instance, in urban planning, minimal path networks help design efficient roadways, pipelines, and utility networks, ensuring that all critical points are connected with minimal infrastructure.

Apparatus for computing minimal path systems, Institute for Lightweight Structures - ILEK, Stuttgart, 1988

Leaf Venation

Venation patterns in plant leaves, responsible for transporting nutrients and providing structural support, have inspired computational models that mimic these natural systems. Researchers like Runions have developed algorithms that simulate the growth of leaf venation, replicating the complex branching patterns found in nature. These models are used not only to study biological processes but also in design, where studios like Nervous System apply them to create nature-inspired objects and structures. By translating the efficiency and beauty of venation into computational forms, designers can explore new ways to incorporate organic principles into their work.

Elevation drawing of installation Summit at Sea

Dijkstra’s algorithm

Dijkstra’s algorithm, developed by Edsger W. Dijkstra in 1956, is a method for finding the shortest paths between nodes in a graph. The algorithm initializes with all nodes set to an infinite distance except the starting node, iteratively visits unvisited nodes, and updates their tentative distances through the current node, marking nodes as visited once their shortest path is determined. This process continues until the shortest path to the destination node is found.

In computational design, Dijkstra’s algorithm is pivotal for various applications. In urban planning and architecture, it determines optimal routes for transportation and emergency evacuations, and in network design, it optimizes data and utility distribution. Robotics utilize it for navigation and resource allocation, while game design employs it for AI pathfinding and level connectivity. Environmental design benefits from its use in creating accessible pathways in parks and ecological corridors, ensuring efficient and sustainable layouts.

A* algorithm

The A* search algorithm, developed in 1968 by Peter Hart, Nils Nilsson, and Bertram Raphael, is a pathfinding and graph traversal algorithm known for its efficiency and accuracy in finding the shortest path from a start node to a goal node. A* combines features of Dijkstra’s algorithm and Greedy Best-First-Search by incorporating both the cost to reach a node and a heuristic estimate of the cost to reach the goal from that node. The algorithm uses a priority queue to explore nodes with the lowest estimated total cost first, ensuring that the most promising paths are evaluated earlier.

Urban planners use it for optimal routing of pedestrian paths and emergency evacuation routes, enhancing connectivity and accessibility. In robotics and autonomous systems, A* enables efficient pathfinding and navigation, crucial for robots to avoid obstacles and reach destinations quickly. Game developers leverage A* for creating realistic AI behavior and dynamic level design, ensuring NPCs navigate game environments intelligently. Additionally, network design benefits from A* in optimizing data flow and infrastructure layout, while landscape architects use it to design efficient trails and pathways in parks, balancing accessibility and environmental conservation.

Medial Axis Route Network Graph

A medial axis route network graph, or medial axis transform (MAT), is a representation of a shape’s central pathways or skeleton, where each point on the skeleton is equidistant from the shape’s boundaries. This graph is composed of nodes representing significant points or junctions and edges that denote the optimal routes between these points within the shape. In computational design, particularly in urban planning, robotics, and game design, the medial axis is invaluable. It facilitates the design of efficient pedestrian pathways in urban environments, aids in optimal path planning for robots by identifying clear, obstacle-free routes, and enhances AI navigation in virtual environments by defining natural movement corridors. Additionally, in landscape architecture, the medial axis guides the creation of scenic trails and ecological corridors, promoting sustainable design practices that balance human use with environmental conservation efforts

Steiner Tree Problem

The Steiner Tree Problem extends the concept of minimal path networks by allowing the addition of intermediate points, known as Steiner points, to further reduce the total length of the network. This problem is particularly challenging due to its NP-hard nature, but various heuristic and approximation algorithms have been developed to find near-optimal solutions.

Wool-Thread Model or Wooly Paths

The wool-thread model, inspired by Frei Otto’s work, emphasizes the organic optimization of structures or networks based on natural forces or flows. In computational design, this approach finds applications in urban design and architectural design.

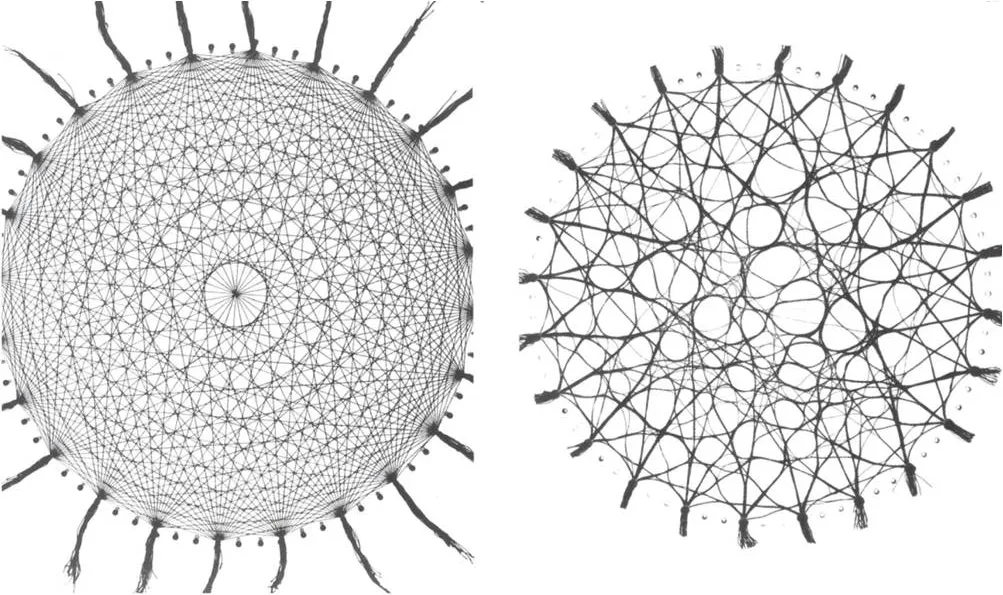This involves taking a network of threads connecting points around a circle and dipping it in water.

You can check read some insights from Frei Otto on this topic in his book Occupying and Connecting.