Otimização de rede

A otimização de rede é uma área crítica em design computacional, com foco na criação de conexões eficientes e econômicas entre um conjunto de pontos. Este campo abrange vários métodos e algoritmos para resolver problemas em telecomunicações, transporte, planejamento urbano e muito mais. Entre os principais conceitos em otimização de rede estão Redes de Caminho Mínimo, o Problema da Árvore de Steiner e Relative Neighborhood Graph.

Relative Neighborhood Graph (RNG)

Relative Neighborhood Graphs (RNGs) conectam pontos com base em sua proximidade relativa, garantindo que uma aresta seja desenhada entre dois pontos se nenhum outro ponto estiver mais próximo de ambos. Esse conceito ajuda a criar redes esparsas que enfatizam conexões locais, que podem então ser usadas como base para otimização posterior.

Animation of a Relative Neighborhood with four anchor points at the corners

Redes de caminhos mínimos

Em inglês Shortest Path Networks and Minimal Path Networks. São fundamentais para garantir que uma rede conectando vários pontos seja a mais curta possível. Por exemplo, no planejamento urbano, redes de caminhos mínimos ajudam a projetar estradas, oleodutos e redes de serviços públicos eficientes, garantindo que todos os pontos críticos sejam conectados com infraestrutura mínima.

Aparelho para computação de sistemas de caminho mínimo, Instituto de Estruturas Leves - ILEK, Stuttgart, 1988

Nervura de folhas

Padrões de venação em folhas de plantas, responsáveis por transportar nutrientes e fornecer suporte estrutural, inspiraram modelos computacionais que imitam esses sistemas naturais. Pesquisadores como Runions desenvolveram algoritmos que simulam o crescimento da venação foliar, replicando os padrões complexos de ramificação encontrados na natureza. Esses modelos são usados não apenas para estudar processos biológicos, mas também em design, onde estúdios como Nervous System os aplicam para criar objetos e estruturas inspirados na natureza. Ao traduzir a eficiência e a beleza da venação em formas computacionais, os designers podem explorar novas maneiras de incorporar princípios orgânicos em seu trabalho.

Elevation drawing of installation Summit at Sea

Algoritmo de Dijkstra’s

O algoritmo de Dijkstra, desenvolvido por Edsger W. Dijkstra em 1956, é um método para encontrar os caminhos mais curtos entre nós em um grafo.

No planejamento urbano e arquitetura, ele determina rotas ideais para transporte e evacuações de emergência, e no design de rede, ele otimiza dados e distribuição de serviços públicos. A robótica o utiliza para navegação e alocação de recursos, enquanto o design de jogos o emprega para localização de caminhos de IA e conectividade de nível. O design ambiental se beneficia de seu uso na criação de caminhos acessíveis em parques e corredores ecológicos, garantindo layouts eficientes e sustentáveis.

Algoritmo A*

O algoritmo A*, desenvolvido em 1968 por Peter Hart, Nils Nilsson e Bertram Raphael, é um algoritmo de busca de caminhos e travessia de grafos conhecido por sua eficiência e precisão em encontrar o caminho mais curto de um nó inicial para um nó de destino. O A* combina recursos do algoritmo de Dijkstra e do Greedy Best-First-Search incorporando tanto o custo para atingir um nó quanto uma estimativa heurística do custo para atingir o objetivo a partir desse nó. O algoritmo usa uma fila de prioridade para explorar nós com o menor custo total estimado primeiro, garantindo que os caminhos mais promissores sejam avaliados antes.

Urbanistas o usam para roteamento ideal de caminhos de pedestres e rotas de evacuação de emergência, melhorando a conectividade e a acessibilidade. Em robótica e sistemas autônomos, o A* permite busca de caminhos e navegação eficientes, cruciais para que os robôs evitem obstáculos e alcancem destinos rapidamente. Os desenvolvedores de jogos aproveitam A* para criar comportamento de IA realista e design de nível dinâmico, garantindo que os NPCs naveguem pelos ambientes do jogo de forma inteligente. Além disso, o design de rede se beneficia de A* na otimização do fluxo de dados e layout de infraestrutura, enquanto arquitetos paisagistas o usam para projetar trilhas e caminhos eficientes em parques, equilibrando acessibilidade e conservação ambiental.

Grafo de rede de rotas do eixo medial

Um grafo de rede de rotas do eixo medial, ou transformação do eixo medial (MAT em inglês), é uma representação dos caminhos centrais ou esqueleto de uma forma, onde cada ponto no esqueleto é equidistante dos limites da forma. Este gráfico é composto de nós que representam pontos significativos ou junções e arestas que denotam as rotas ideais entre esses pontos dentro da forma. No design computacional, particularmente no planejamento urbano, robótica e design de jogos, o eixo medial é inestimável. Ele facilita o design de caminhos de pedestres eficientes em ambientes urbanos, auxilia no planejamento de caminhos ideais para robôs ao identificar rotas claras e sem obstáculos e aprimora a navegação de IA em ambientes virtuais ao definir corredores de movimento natural. Além disso, na arquitetura paisagística, o eixo medial orienta a criação de trilhas cênicas e corredores ecológicos, promovendo práticas de design sustentáveis que equilibram o uso humano com os esforços de conservação ambiental

Problema da Árvore de Steiner

O Problema da Árvore de Steiner estende o conceito de redes de caminhos mínimos ao permitir a adição de pontos intermediários, conhecidos como pontos de Steiner, para reduzir ainda mais o comprimento total da rede. Este problema é particularmente desafiador devido à sua natureza NP-difícil, mas vários algoritmos heurísticos e de aproximação foram desenvolvidos para encontrar soluções quase ótimas.

Modelo com Fio de Lã

O modelo de fio de lã, inspirado no trabalho de Frei Otto, enfatiza a otimização orgânica de estruturas ou redes com base em forças naturais. No design computacional, essa abordagem encontra aplicações em planejamento urbano e design arquitetônico.

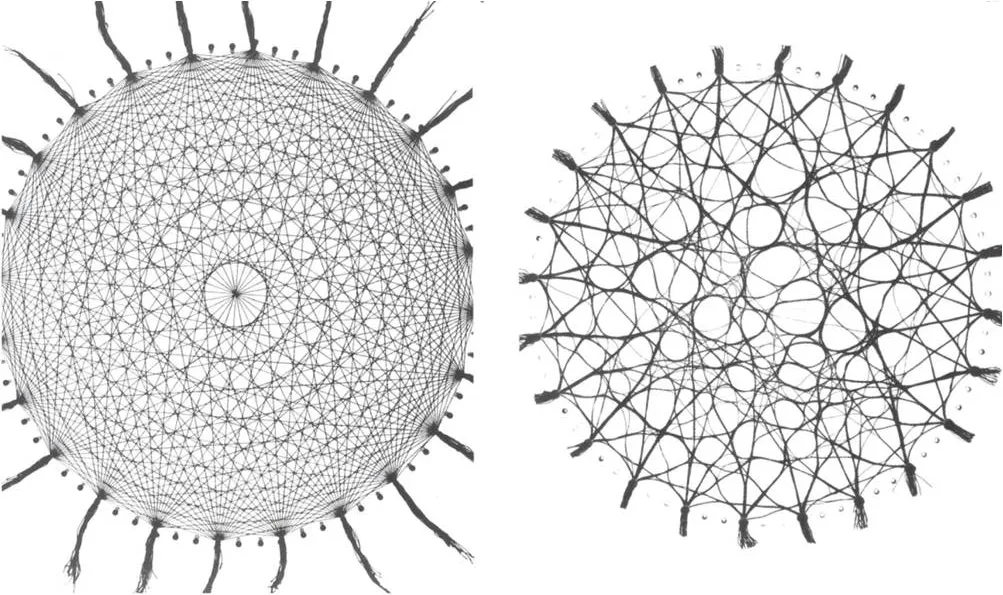Isso envolve pegar uma rede de fios conectando pontos ao redor de um círculo e mergulhá-la em água.

Você pode conferir alguns insights de Frei Otto sobre esse tópico em seu livro Occupying and Connecting.